I am interested in a wide range of topics related to quantum information theory. It started with my PhD thesis on “Quantum state discrimination with Gaussian states" with Seth Lloyd at MIT in which I worked on a class of continuous variable states, the Gaussian states, for applications in quantum metrology and quantum communication. Following my graduation in 2010, I started working at the Data Storage Institute (A*STAR, Singapore) on industry-applied problems focusing on quantum optical applications of quantum information theory using photon-pairs produced by non-linear photonic crystals and semi-conductor photon-number-resolving detectors. In 2013, I joined the group of Joseph Fitzsimons where I switched gears to look into constructing new quantum cryptographic protocols for secure delegated quantum computing.
Here is a summary of my research:
(1) Secure delegated quantum computing
Quantum homomorphic encryption: In the world of classical cryptography, homomorphic encryption has been a hot research topic since the discovery of a fully homomorphic encryption scheme by Gentry in 2009. Homomorphic encryption is a cryptographic primitive that allows for the processing of ciphertext without revealing the key that is used for encryption to the processor. The plaintext is never revealed to the server, and hence kept secure. I have been designing quantum encryption-decryption, and processing algorithms to implement quantum homomorphic encryption for data represented on quantum states. The advantages of such quantum schemes is two-fold. First, they have information theoretic security which is not premised on any hardness assumptions. Second, the class of quantum computations that can be performed may include stuff that is hard to simulate on classical computers.
Multi-user blind quantum computing: Blind quantum computing (BQC) is a quantum cryptographic scheme that allows a client to delegate quantum computations on quantum data to a remote server without revealing the computation, nor the input state. I have been working on an extension of BQC to allow multiple clients to delegate parts of a quantum computations to a single server. No information about each client’s part is revealed to the other clients, and as in BQC, the server does not learn the computation nor the input state. By working in the abstract cryptography framework, the security derives from the composable security of each algorithm used in the multi-user BQC scheme.
(2) Quantum interferometry of single photons
Photons scatter through an interferometer just like fermions would in potential fields. Although they do not couple to one another, many interesting quantum mechanical effects can occur when they pass through these interferometers. One such effect is the Hong-Ou-Mandel dip, sometimes known as photon-bunching, in which two identical single photons that impinge on a beamsplitter with one photon in each input tends to emerge together and the coincidence (one photon in each outcome) is extinguished. I am interested in the generalization of these types of effects, specifically in the case when the photons are non-identical and applications of these effects to linear optical quantum computing, and other classically hard-to-simulate tasks like boson-sampling.
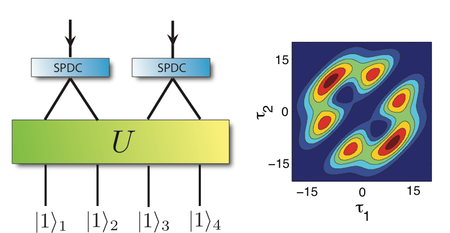
(2) Quantum optics: Photon-counting
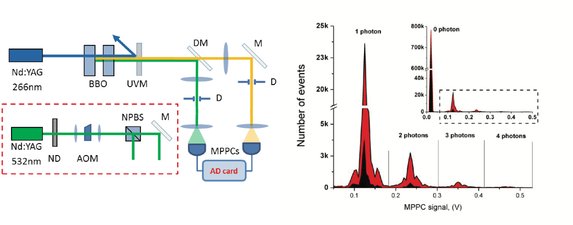
Many technological applications of quantum optics require the use of photon-number-resolving detectors (PNRDs) which are named for their ability to resolve between N and N+1 photons, for N>1. However, these PNRDs suffer from noise and losses. I look at how these artifacts influence measurement of quantum correlations, such as g(2) and higher-order correlations, and the noise reduction factor.
(4) Quantum measurements and decoding
Optical communication using quantum states through quantum channels is an interesting extension of the classical Gaussian channels. To be able to harness the quantum advantage afforded by preparing and using states and channels, we have to construct explicit receivers which are immediately implementable using available known methods from classical coding, non-linear optics and sequential waveform nulling.